Pinwheel Tiling
This manipulative allows tiling the plane with Pinwheel Triangles. A Pinwheel Triangle is a right triangle with one leg twice as long as the other. Five Pinwheel Triangles can be combined to form a larger Pinwheel Triangle, called a super-tile, with the original triangle occupying the interior position in the arrangement shown below:
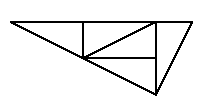
Click the Triangle button to put a Pinwheel Triangle into the workspace. A triangle can be moved by clicking and dragging it to a new location. To rotate a triangle, click and drag any of its vertices.
Triangles can be grouped by clicking and dragging to draw a rectangle around the group. Once grouped, triangles can be ungrouped by holding down the Shift key while dragging a rectangle around the group.
For tiling the plane, a efficient tiling process is available. With a triangle selected in the workspace, click to create a super-tile consisting of five triangles, with the original triangle occupying the interior position. Clicking undoes the super-tile construction, reducing an arrangement to its interior triangle. Repeatedly clicking the builds larger and larger super-tiles as part of the pinwheel tiling for the entire plane.
At any stage, it is possible to duplicate a selected triangle or group by clicking .
Background information:
The pinwheel tiling is a remarkable example (due to John Conway of Princeton University and Charles Radin of the University of Texas, Austin) of a tiling of the plane by copies of a single right triangle. Of course, two copies of any right triangle can be glued together along their common hypotenuse to form a rectangle, and copies of any rectangle can be easily seen to tile the plane in a most regular fashion. The Conway/Radin pinwheel tiling, though, has two very unusual properties, called symmetry of scale, and no rigid symmetries.
Symmetry of scale means that the tiling may be considered as increasingly large blocks that are all copies of the same basic shape. These blocks are sometimes called super-tiles, so that for the pinwheel tiling, five triangles fit together to form a super-tile, and five such super-tile fit together in the same way to make a larger super-tile containing twenty-five of the original triangles.
That there are no rigid symmetries in this tiling means essentially that every triangle fits into the pattern in just one way. That is, if you were to take two copies of the tiling, say on two transparent pages, then there is only one way to put one of the copies on top of the other to make a given pair of triangles match and have the rest of the triangles line up. Compare that uniqueness with the freedom you would have to line up a regular tiling made up of triangles paired into rectangles.