
Información para Profesores: Solucionador de Triángulos
Muchos de los problemas de ciencia e ingeniería se pueden resolver usando las relaciones propias de los triángulos. Aquí se presentan dos ejemplos sencillos:
1. Para determinar la altura de una montaña, un explorador toma dos vistas del pico. Las primeras observaciones arrojan un ángulo de elevación de 46 grados; las segundas observaciones arrojan un ángulo de 34 grados. La distancia entre los dos puntos de observación es de 800 metros, como se muestra en el diagrama.

¿Cuál en la altura de la montaña?
Para responder esta pregunta, se necesita organizar los datos matemáticamente, como lo muestran los triángulos en el diagrama. Luego, utilizando el Teorema del Seno, se puede hallar la altura de la montaña.
2. Dos buques zarpan de un mismo puerto a las 7 a.m. Uno navega en dirección N 55º O (55 grados al oeste del norte) a 15 millas por hora, y el segundo avanza a 11 millas por hora en dirección S 65º O (65 grados al oeste del sur).
¿Cuál es la distancia aproximada entre ambos buques a las 11 a.m.?
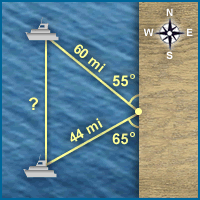
El diagrama muestra esta situación matemáticamente. Usando el Teorema del Coseno, se puede encontrar la distancia que separa a los buques.
Estas y muchas otras aplicaciones pueden describirse matemáticamente dibujando un triángulo e identificando los lados y los ángulos conocidos. La respuesta se encuentra determinando los valores de los lados y ángulos restantes.
Este manipulador muestra un triángulo con los valores de algunos de sus lados y ángulos. El estudiante debe determinar el valor de los lados y ángulos restantes. Para lograrlo se debe escoger una estrategia y usar el Teorema de Pitágoras o las relaciones de seno, coseno y tangente, o el Teorema del Seno, o el Teorema del Coseno. En todo momento el manipulador guiará a los estudiantes a dar los pasos claves hasta encontrar los lados y ángulos desconocidos.
El paso 1 consiste en escoger el lado o el ángulo desconocido que desea encontrar.
El paso 2 consiste en escoger un método que dé como resultado una ecuación que permita obtener el valor desconocido.
El paso 3 consiste en completar la ecuación que corresponde al método escogido.
El paso 4 consiste en calcular y escribir el resultado.
Durante cada paso, el estudiante recibe avisos y consejos a fin de que pueda entender mejor las relaciones de los triángulos y las estrategias de solución.