Instructions pour l’enseignant : Solutionneur de triangles

Plusieurs problèmes appliqués en science et en ingénierie peuvent être résolus grâce aux relations trigonométriques impliquant les côtés et les angles des triangles. Voici deux exemples simples :

1. Afin de déterminer la hauteur d’une montagne, un ingénieur topographe prend deux clichés du sommet. Les premières observations donnent comme résultat un angle d’élévation de 46 degrés; les secondes observations donnent comme résultat un angle de 34 degrés. La distance entre les deux points d’observation est de 800 mètres, tel que l’indique le diagramme.

Quelle hauteur a la montagne?

Pour répondre à cette question, tu devras décrire la situation de façon mathématique, tel que le démontrent les triangles dans le diagramme. Ensuite, en utilisant la loi des sinus, tu pourras déterminer la hauteur de la montagne.

2. Deux navires quittent le port à 7 h. L’un a un cap de N 55º O (55 degrés à l’ouest du nord) et une vitesse de 15 kilomètres-heure et le second a un cap de S 65º O (65 degrés à l’ouest du sud) et se déplace à une vitesse de 11 kilomètres-heure.

À 11 h, quelle sera la distance approximative entre les navires?

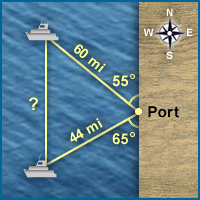
Le diagramme offre une description mathématique de la situation. Utilise la loi des cosinus pour trouver la distance qui sépare les deux navires.

Ces applications et plusieurs autres encore peuvent être décrites mathématiquement en dessinant un triangle et en identifiant les côtés et les angles connus. La solution est obtenue en déterminant les valeurs des côtés et des angles manquants.

L’activité virtuelle de manipulation du Solutionneur de triangles illustre un triangle dont les mesures de certains côtés et angles sont données. Tu dois ensuite déterminer les valeurs correspondant aux côtés et angles manquants. En choisissant une stratégie valable et en utilisant le théorème de Pythagore, les relations sinus, cosinus, tangente, ou la loi des sinus ou des cosinus, tu seras guidé au fil des étapes clés qui te permettront de découvrir les côtés et angles inconnus.

L’Étape 1 consiste à choisir le côté ou l’angle inconnu à identifier

L’Étape 2 consiste à choisir une méthode offrant une équation qui lui permettra de trouver la valeur de l’inconnu sélectionné

L’Étape 3 consiste à compléter l’équation qui correspond à la méthode choisie

L’Étape 4 consiste à effectuer le calcul nécessaire et à indiquer le résultat.

À chaque étape, une rétroaction instantanée est fournie pour aider l’élève à mieux comprendre les relations triangulaires et les stratégies de résolution.