所有主题 (年级 六年级到八年级(初中))

下面的虚拟操作器适用的年级：六年级到八年级(初中)。

数字和运算 (年级 六年级到八年级(初中))

	Diffy 模拟操作 – 解决一道有趣的难题, 即计算所给定的数的差。
	七巧板 – 使用源于中国的七块小拼块来构成不同的形状及解决问题。
	乌龟几何学 – 通过程序设计使乌龟移动来探究数字， 图形， 和逻辑。
	决斗计算器 – 形象化地对舍入误差传递的影响进行生动的模拟。
	函数图像 – 一个绘制及探究函数的工具。
	函数机器 – 通过将数值放入这个机器中并观察其输出的值来探究函数的概念。
	分数数轴长条 – 使用数轴长条除以分数。
	分数模块 – 用部分和整体来学习分数。
	分数的加法 – 说明找出公分母及合并的意思。
	分数的矩阵乘法 – 使用面积表示法来形象化地观察和练习分数乘法。
	因子树 – 用树图来分解因子。
	圆圈 0 – 一道关于相加正负整数至和为零的难题。
	圆圈 21 – 一道关于相加正负整数得到和为21的难题。
	圆圈 3 – 一道关于相加正实数得到和为3的难题。
	圆圈 99 – 一道关于相加正负整数得到和为99的难题。
	圆片算盘 – 用圆片学习进位和数位。
	埃拉托斯特尼筛选法 – 将数字的模式和视觉的模式联系起来。
	帕斯卡三角形 – 通过选择帕斯卡三角形中的元素来探究建立的模式。
	底数块 – 说明不同底数下的加法和减法。
	底数块减法 – 用底数10方块来建立减法中分开组合的模型。
	底数块加法 – 用底数10方块来建立加法中组合的模型。
	底数块小数 – 用底数块相加及相减小数值。
	康韦的生命游戏 – 探索决定这些模拟中的变化的规律。
	数字难题 – 通过在一个图表中排列数字， 使这些数字相加的和等于一个给定的值来解决数字难题。
	数轴跳跃 – 数轴上的加法和减法游戏。
	文氏图表 – 调查学习集合的通常特征。
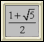	斐波那契数列 – 探究斐波那契数列和黄金分割率。
	智多星 – 使用推理和逻辑来玩游戏并猜测图钉的隐藏的模式。
	木桩难题 – 通过移动木桩将左边的木桩和右边的木桩交换位置来赢得这个游戏。
	比较分数 – 判断分数的大小并将它们绘制在数轴上。
	百分数 – 发现分数， 百分数， 和小数之间的关系。
	百分率格表 – 展示、命名以及使用百格表来探索百分率。
	等值分数 – 说明等值分数间的关系。
	算盘 – 一个电子版的算盘， 能用来做算术。
	细密的编织法 – 形象化地显示"塞尔平斯基地毯"的创制过程， 即通过一个重复的几何模式来生成一个编织毯。
	色彩方片 - 减法 – 用色彩方片来说明整数的减法。
	货币金额 – 通过计数货币和找零钱来学习货币金额。
	转盘 – 通过练习使用转盘来学习数字和概率。
	黄金矩形 – 说明黄金区域的迭代。

代数 (年级 六年级到八年级(初中))

	三角形骨牌 – 对三角形拼块进行操作， 来找到多种解决方法。
	五连方拼块 – 使用十二个五连方拼块进行组合来解决问题。
	函数变换 – 探索简易的函数方程式变换如何影响图形的改变。
	函数图像 – 一个绘制及探究函数的工具。
	函数机器 – 通过将数值放入这个机器中并观察其输出的值来探究函数的概念。
	十五难题 – 用排列方砖来解决经典的十五难题的形象化版本。
	因子树 – 用树图来分解因子。
	坚持还是改变 – 调查学习一下哪种策略获胜的机率大： 坚持一种选择的策略还是改变上次选择的策略。
	底数块 – 说明不同底数下的加法和减法。
	方块模式 – 使用图片、表格、平面图、以及图表来分析一列的图形。
	木桩难题 – 通过移动木桩将左边的木桩和右边的木桩交换位置来赢得这个游戏。
	模式方块 – 使用六个普通的几何形状来构造模式及解决问题。
	汉诺塔问题 – 解决这个移动圆盘的问题， 并通过改变所需移动圆盘的数量来测试你的理论。
	点绘图器 – 练习绘制已知成对点的图形。
	硬币问题 – 用推论找出伪造的硬币。
	空间立体方块 – 使用三维的立体方块来创建和发现模式。
	算术天平 – 用平衡天平的象征来解简单的线性方程式。
	算术天平 —— 负数 – 用天平平衡的象征来解简单的线性方程式。
	算术砖 – 用算术砖来形象化地演示算术表达式的相乘和因子分解。
	线绘图操作器 – 练习绘制通过一个已知坐标点、且具特定斜率的直线。
	骨牌游戏 – 构造和比较两格骨牌， 三格骨牌， 四格骨牌等等的各自特色。

几何 (年级 六年级到八年级(初中))

	Koch曲线和Sierpinski地毯分形 – 改变颜色， 可以随时暂停这种分形模拟。
	Mandelbrot-Julia集合 – 研究这两种分形集合间的关系。
	七巧板 – 使用源于中国的七块小拼块来构成不同的形状及解决问题。
	三角形骨牌 – 对三角形拼块进行操作， 来找到多种解决方法。
	乌龟几何学 – 通过程序设计使乌龟移动来探究数字， 图形， 和逻辑。
	五连方拼块 – 使用十二个五连方拼块进行组合来解决问题。
	交互分形 – 生成六种不同的分形。
	全等三角形 – 通过合并边和角来组成全等三角形。
	几何面板 – 用几何面板说明面积，周长，及有理数的概念。
	变换　－　反射 – 动态地互动操作反射变换并观察反射变换的结果。
	变换　－　合成 – 探究对物体运用平移， 旋转， 和反射合成变换的效果。
	变换　－　平移 – 动态地互动操作平移变换并观察平移变换的结果。
	变换　－　旋转 – 动态地互动操作旋转变换并观察旋转变换的结果。
	变换　－　缩放 – 动态地互动操作缩放变换并观察缩放变换的结果。
	圆形几何面板 – 用圆形几何面板来说明角及其度数。
	坐标几何面板 – 带有 x 和 y 坐标的矩形面板。
	多边形分形 – 改变参数来创建一个新的分形。
	多高？ – 以经典的皮亚杰（Piagetian）容量测试保留概念， 做一下猜测。
	大圆 – 使用一个三维的地球仪来形象化地显示和测量两个城市间的最短路径。
	属性火车 – 通过完成属性块火车来学习图形及颜色的模式。
	拼块镶嵌 – 使用规则的和半规则的拼块镶嵌来铺设平面区域。
	柏拉图固体 – 识别柏拉图固体的特性。
	柏拉图固体-切割 – 观察发现形状及柏拉图固体切面间的关系。
	柏拉图固体-双数 – 确认柏拉图固体的双数对应。
	模式方块 – 使用六个普通的几何形状来构造模式及解决问题。
	毕达哥拉斯定理 – 解决演示证明勾股定理的两个拼图问题。
	瓢虫叶 – 通过一个程序设计出如何将瓢虫藏在叶子后面。
	瓢虫迷宫 – 通过一个程序设计出如何让瓢虫在迷宫中移动。
	空间立体方块 – 使用三维的立体方块来创建和发现模式。
	等角几何面板 – 用几何面板来说明三维图形。
	细密的编织法 – 形象化地显示"塞尔平斯基地毯"的创制过程， 即通过一个重复的几何模式来生成一个编织毯。
	蛛网图 – 改变变量并从这个绘制的模拟中观察形成的模式。
	骨牌游戏 – 构造和比较两格骨牌， 三格骨牌， 四格骨牌等等的各自特色。
	黄金矩形 – 说明黄金区域的迭代。

测量 (年级 六年级到八年级(初中))

	七巧板 – 使用源于中国的七块小拼块来构成不同的形状及解决问题。
	几何面板 – 用几何面板说明面积，周长，及有理数的概念。
	单位换算 – 用一个简单的系统来换算单位。
	圆形几何面板 – 用圆形几何面板来说明角及其度数。
	填充和倒出 – 解决要填满和倒空容器的难题。
	多高？ – 以经典的皮亚杰（Piagetian）容量测试保留概念， 做一下猜测。
	大圆 – 使用一个三维的地球仪来形象化地显示和测量两个城市间的最短路径。
	属性火车 – 通过完成属性块火车来学习图形及颜色的模式。
	时间 - 将会是几点钟？ – 回答对你提出的问题： 指出在指定时间之前或之后的一段时间将会是几点钟。
	模式方块 – 使用六个普通的几何形状来构造模式及解决问题。
	瓢虫叶 – 通过一个程序设计出如何将瓢虫藏在叶子后面。
	瓢虫迷宫 – 通过一个程序设计出如何让瓢虫在迷宫中移动。
	货币金额 – 通过计数货币和找零钱来学习货币金额。

资料分析和机率 (年级 六年级到八年级(初中))

	哈姆莱特剧本的发生 – 通过从一个盒子中抽取字母来证实罕见事件可能发生。
	坚持还是改变 – 调查学习一下哪种策略获胜的机率大： 坚持一种选择的策略还是改变上次选择的策略。
	存款计算器 – 探究如何在一段时间内， 通过定期或不定期存款使储蓄额增长。
	抽奖箱模型 – 随机选择及显示从箱中抽奖的过程。
	掷硬币 – 通过模拟反复的掷硬币过程来探究概率的概念。
	散点图 – 对多个数据点绘制两维图并决定两个变量间的关系。
	条状图表 – 通过命名列及点击值来创建一个显示数量及百分比的条状图表。
	箱形图 / 柱状图 – 使用这个工具来用一个箱形图总结数据。
	箱形图 / 柱状图 – 使用这个工具来用一个柱状图总结数据。
	贷款计算器 – 探究如何偿付一笔贷款， 及利率对付款的影响。
	转盘 – 通过练习使用转盘来学习数字和概率。
	饼图 – 使用饼图来探究百分比和分数的概念。