Number & Operations (Grades 9 - 12)

Virtual manipulatives for Number & Operations, grades 9 - 12.

	Abacus – An electronic abacus that can be used to do arithmetic.
	Circle 0 – A puzzle involving adding positive and negative integers to sum to zero.
	Circle 21 – A puzzle involving adding positive and negative integers to sum to twenty one.
	Circle 3 – A puzzle involving adding positive real numbers to sum to three.
	Circle 99 – A puzzle involving adding positive and negative integers to sum to ninety nine.
	Conway's Game of Life – Discover the rules that determine change in these simulations.
	Counting All Pairs – Create a path that sets up a one-to-one correspondence between the counting numbers and infinite sets of ordered pairs of integers.
	Diffy – Solve an interesting puzzle involving the differences of given numbers.
	Dueling Calculators – Visualize a dramatic simulation of the effect of propagating rounding errors.
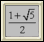	Fibonacci Sequence – Explore the Fibonacci sequence and the golden ratio.
	Fractions - Adding – Illustrates what it means to find a common denominator and combine.
	Fractions - Equivalent – Illustrates relationships between equivalent fractions.
	Function Machine – Explore the concept of functions by putting values into this machine and observing its output.
	Golden Rectangle – Illustrates iterations of the Golden Section.
	Grapher – A tool for graphing and exploring functions.
	Mastermind – Use inference and logic to play a game and guess a hidden pattern of pegs.
	Number Puzzles – Solve puzzles involving arranging numbers on a diagram so that they add up to a given value.
	Pascal's Triangle – Explore patterns created by selecting elements of Pascal's triangle.
	Peg Puzzle – Win this game by moving the pegs on the left past the pegs on the right.
	Percentages – Discover relationships between fractions, percents, and decimals.
	Rational Numbers Triangle – Explore a triangular array that contains every positive rational number exactly once.
	Sieve of Eratosthenes – Relate number patterns with visual patterns.
	Tight Weave – Visualize the creation of the Sierpinski Carpet, an iterative geometric pattern that resembles a woven mat.
	Turtle Geometry – Explore numbers, shapes, and logic by programming a turtle to move.
	Venn Diagrams – Investigate common features of sets.