All Topics (Grades 9 - 12)

Virtual manipulatives for grades 9 - 12.

Number & Operations (Grades 9 - 12)

	Abacus – An electronic abacus that can be used to do arithmetic.
	Circle 0 – A puzzle involving adding positive and negative integers to sum to zero.
	Circle 21 – A puzzle involving adding positive and negative integers to sum to twenty one.
	Circle 3 – A puzzle involving adding positive real numbers to sum to three.
	Circle 99 – A puzzle involving adding positive and negative integers to sum to ninety nine.
	Conway's Game of Life – Discover the rules that determine change in these simulations.
	Counting All Pairs – Create a path that sets up a one-to-one correspondence between the counting numbers and infinite sets of ordered pairs of integers.
	Diffy – Solve an interesting puzzle involving the differences of given numbers.
	Dueling Calculators – Visualize a dramatic simulation of the effect of propagating rounding errors.
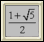	Fibonacci Sequence – Explore the Fibonacci sequence and the golden ratio.
	Fractions - Adding – Illustrates what it means to find a common denominator and combine.
	Fractions - Equivalent – Illustrates relationships between equivalent fractions.
	Function Machine – Explore the concept of functions by putting values into this machine and observing its output.
	Golden Rectangle – Illustrates iterations of the Golden Section.
	Grapher – A tool for graphing and exploring functions.
	Mastermind – Use inference and logic to play a game and guess a hidden pattern of pegs.
	Number Puzzles – Solve puzzles involving arranging numbers on a diagram so that they add up to a given value.
	Pascal's Triangle – Explore patterns created by selecting elements of Pascal's triangle.
	Peg Puzzle – Win this game by moving the pegs on the left past the pegs on the right.
	Percentages – Discover relationships between fractions, percents, and decimals.
	Rational Numbers Triangle – Explore a triangular array that contains every positive rational number exactly once.
	Sieve of Eratosthenes – Relate number patterns with visual patterns.
	Tight Weave – Visualize the creation of the Sierpinski Carpet, an iterative geometric pattern that resembles a woven mat.
	Turtle Geometry – Explore numbers, shapes, and logic by programming a turtle to move.
	Venn Diagrams – Investigate common features of sets.

Algebra (Grades 9 - 12)

	Algebra Balance Scales – Solve simple linear equations using a balance beam representation.
	Algebra Balance Scales - Negatives – Solve simple linear equations using a balance beam representation.
	Algebra Tiles – Visualize multiplying and factoring algebraic expressions using tiles.
	Base Blocks – Illustrate addition and subtraction in a variety of bases.
	Block Patterns – Analyze sequences of figures using pictures, tables, plots, and graphs.
	Coin Problem – Use deduction to find the counterfeit coin.
	Fifteen Puzzle – Solve this virtual version of the classical fifteen puzzle by arranging its tiles.
	Function Machine – Explore the concept of functions by putting values into this machine and observing its output.
	Function Transformations – Explore how simple transformations affect the graph of a function.
	Grapher – A tool for graphing and exploring functions.
	Line Plotter – Practice drawing lines through a given point having a specified slope.
	Pattern Blocks – Use six common geometric shapes to build patterns and solve problems.
	Peg Puzzle – Win this game by moving the pegs on the left past the pegs on the right.
	Pentominoes – Use the 12 pentomino combinations to solve problems.
	Point Plotter – Practice plotting ordered pairs on a graph.
	Polyominoes – Build and compare characteristics of biominoes, triominoes, quadrominoes, etc.
	Stick or Switch – Investigate probabilities of sticking with a decision, or switching.
	Towers of Hanoi – Solve the tower problem and test your theory by varying the number of disks.

Geometry (Grades 9 - 12)

	Cob Web Plot – Change variables and observe patterns from this graphing simulation.
	Fractals - Iterative – Generate six different fractals.
	Fractals - Koch and Sierpinski – Change colors and pause this fractal simulation at any point.
	Fractals - Mandelbrot and Julia Sets – Investigate relationships between these two fractal sets.
	Fractals - Polygonal – Change the parameters to create a new fractal.
	Geoboard – Use geoboards to illustrate area, perimeter, and rational number concepts.
	Geoboard - Circular – Use circular geoboards to illustrate angles and degrees.
	Geoboard - Coordinate – Rectangular geoboard with x and y coordinates.
	Geoboard - Isometric – Use geoboard to illustrate three-dimensional shapes.
	Golden Rectangle – Illustrates iterations of the Golden Section.
	Great Circle – Use a 3D globe to visualize and measure the shortest path between cities.
	Pattern Blocks – Use six common geometric shapes to build patterns and solve problems.
	Pinwheel Tiling – Construct and explore a very unusual tiling of the plane by right triangles.
	Platonic Solids – Identify characteristics of the Platonic Solids.
	Platonic Solids - Duals – Identify the duals of the platonic solids.
	Platonic Solids - Slicing – Discover shapes and relationships between slices of the platonic solids.
	Polyominoes – Build and compare characteristics of biominoes, triominoes, quadrominoes, etc.
	Pythagorean Theorem – Solve two puzzles that illustrate the proof of the Pythagorean Theorem.
	Right Triangle Solver – Practice using the Pythagorean theorem and the definitions of the trigonometric functions to solve for unknown sides and angles of a right triangle.
	Space Blocks – Create and discover patterns using three dimensional blocks.
	Tangrams – Use all seven Chinese puzzle pieces to make shapes and solve problems.
	Tessellations – Using regular and semi-regular tessellations to tile the plane.
	Tight Weave – Visualize the creation of the Sierpinski Carpet, an iterative geometric pattern that resembles a woven mat.
	Transformations - Composition – Explore the effect of applying a composition of translation, rotation, and reflection transformations to objects.
	Transformations - Dilation – Dynamically interact with and see the result of a dilation transformation.
	Transformations - Reflection – Dynamically interact with and see the result of a reflection transformation.
	Transformations - Rotation – Dynamically interact with and see the result of a rotation transformation.
	Transformations - Translation – Dynamically interact with and see the result of a translation transformation.
	Triangle Solver – Practice using the law of sines and the law of cosines to solve for unknown sides and angles of a triangle.
	Turtle Geometry – Explore numbers, shapes, and logic by programming a turtle to move.

Measurement (Grades 9 - 12)

	Converting Units – Use a simple system for converting units.
	Fill and Pour – Solve puzzles requiring you to fill and pour containers.
	Geoboard – Use geoboards to illustrate area, perimeter, and rational number concepts.
	Geoboard - Circular – Use circular geoboards to illustrate angles and degrees.
	Great Circle – Use a 3D globe to visualize and measure the shortest path between cities.
	How High? – Try your hand at the classic Piagetian conservation of volume test.
	Pattern Blocks – Use six common geometric shapes to build patterns and solve problems.

Data Analysis & Probability (Grades 9 - 12)

	Bar Chart – Create a bar chart showing quantities or percentages by labeling columns and clicking on values.
	Box Model – Randomly selects and displays draws from a box.
	Box Plot – Use this tool to summarize data using a box plot graph.
	Coin Tossing – Explore probability concepts by simulating repeated coin tosses.
	Hamlet Happens – Verify that rare events happen by drawing letters from a box.
	Histogram – Use this tool to summarize data using a histogram graph.
	Loan Calculator – Explore how to pay off a loan, and how interest affects payment.
	Pascal's Triangle – Explore patterns created by selecting elements of Pascal's triangle.
	Pie Chart – Explore percentages and fractions using pie charts.
	Savings Calculator – Explore how savings, with or without regular deposits, grow over time.
	Scatterplot – Plot multiple data points in two dimensions and determine correlation.
	Spinners – Work with spinners to learn about numbers and probabilities.
	Stick or Switch – Investigate probabilities of sticking with a decision, or switching.
	Whammy Awards – See how using different voting schemes can result in contradictory outcomes.