 |
Abaque – Utiliser un abaque électronique pour réaliser des opérations arithmétiques. |
 |
Casse-tête numériques – Résoudre un casse-tête qui consiste à additionner des chiffres sur un diagramme pour obtenir une somme donnée. |
 |
Cercle 0 – Additionner des nombres entiers positifs et négatifs pour obtenir une somme égale à 0. |
 |
Cercle 21 – Additionner des nombres entiers positifs et négatifs pour obtenir une somme égale à 21. |
 |
Cercle 3 – Additionner des nombres réels positifs pour obtenir une somme égale à 3. |
 |
Cercle 99 – Additionner des nombres entiers positifs et négatifs pour obtenir une somme égale à 99. |
 |
Compter toutes les paires – Créer un chemin qui passe par des points du plan définis par une paire de nombres entiers (cordonnées). |
 |
Crible d'Ératosthène – Etablir une relation entre des motifs numériques et des motifs visuels. |
 |
Diagrammes de Venn – Etudier les caractéristiques communes de plusieurs ensembles. |
 |
Diffy – Résoudre un casse-tête concernant des différences entre des nombres donnés. |
 |
Duel de calculateurs – Visualiser la propagation des erreurs d'arrondissement. |
 |
Fractions - Addition – Illustrer la signification du dénominateur commun et créer des combinaisons. |
 |
Fractions - Équivalence – Illustrer les relations entre des fractions équivalentes. |
 |
Graphiques de fonctions – Tracer et explorer les graphiques de fonctions. |
 |
Géométrie de la tortue – Explorer les nombres, les formes et la logique en créant un programme pour faire bouger une tortue. |
 |
Jeu de chevilles – Gagner ce jeu en déplacant les chevilles de droite vers la gauche et vice-versa. |
 |
Le jeu de la vie de John Conway – Découvrir les règles qui font évoluer la simulation. |
 |
Machine à fonctions – Explorer le concept de fonction en indiquant des valeurs à la machine et en observant le résultat. |
 |
Mastermind – Utiliser la déduction et la logique pour deviner la couleur des fiches cachées. |
 |
Pourcentages – Découvrir le rapport entre fractions, pourcentages et nombres décimaux. |
 |
Rectangle d'or – Visualiser les itérations du rectangle d'or. |
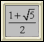 |
Suite de Fibonacci – Explorer la série de Fibonacci et le nombre d'or. |
 |
Tissage – Visualiser la création du tapis de Sierpinski, un motif itératif qui ressemble à un tissage. |
 |
Triangle de Pascal – Explorer des motifs créés en créant des configurations dans le triangle de Pascal. |
 |
Triangle de nombres rationnels – Explorer un tableau triangulaire qui contient chaque nombre rationnel positif une seule fois. |
 |
Balance algébrique – Résoudre des équations linéaires simples en utilisant une balance virtuelle. |
 |
Balance algébrique - Valeurs négatives – Résoudre des équations linéaires simples en utilisant une balance virtuelle. |
 |
Blocs de base – Illustrer l'addition et la soustraction dans différentes bases. |
 |
Blocs de motif – Utiliser des formes géométriques habituelles pour construire des configurations et résoudre des problèmes. |
 |
Blocs de motifs – Analyse des suites de figures en utilisant des images, des tableaux et des graphiques. |
 |
Carreaux algébriques – Visualiser des expressions algébriques (multiplication, puissance) en utilisant des carreaux algébriques. |
 |
Fausse monnaie – Utiliser la déduction pour découvrir la fausse pièce de monnaie. |
 |
Graphiques de fonctions – Tracer et explorer les graphiques de fonctions. |
 |
Jeu de chevilles – Gagner ce jeu en déplacant les chevilles de droite vers la gauche et vice-versa. |
 |
Machine à fonctions – Explorer le concept de fonction en indiquant des valeurs à la machine et en observant le résultat. |
 |
Pentominos – Utiliser les 12 combinaisons de pentominos pour résoudre des problèmes. |
 |
Persister ou changer – Etudier la probabilité de perdre ou de gagner selon le choix de la stratégie. |
 |
Polyominos – Construire des biominos, triominos, quadrominos; etc., et comparer leurs caractéristiques. |
 |
Quinze carreaux – Rérranger les carreaux numérotés dans un certain ordre en les déplaçant un à un. |
 |
Tours de Hanoi – Reconstruire la tour de Hanoi et tester sa connaissance théorique en changeant le nombre de disques. |
 |
Traceur de lignes – Exerce-toi à tracer des lignes selon une pente spécifique, en passant par un point donné. |
 |
Traceur de points – Exerce-toi à tracer des paires ordonnées sur un graphique. |
 |
Transformations de fonctions – Explore comment de simples transformations affectent le graphique d'une fonction |
 |
Blocs de motif – Utiliser des formes géométriques habituelles pour construire des configurations et résoudre des problèmes. |
 |
Conversion des unités – Utiliser un système simple pour convertir des unités. |
 |
Géoplan – Utiliser des géoplans pour illustrer les concepts de surface, de périmètre et de nombre rationnel. |
 |
Géoplan circulaire – Utiliser des géoplans circulaires pour illustrer les concepts d'angle et de degré. |
 |
Orthodromie – Utiliser un globe en 3 dimensions pour visualiser et mesurer le chemin le plus court entre deux villes. |
 |
Quel niveau ? – Apprendre la loi de la conservation des volumes en versant le liquide d'un conteneur dans un autre de forme différente. |
 |
Remplir et verser – Résoudre un casse-tête en remplissant, vidant et transvidant un liquide entre deux contenants. |
 |
Cadran du hasard – Etudier les nombres et les probabilités en jouant au cadran. |
 |
Calculateur d'épargnes – Explorer l'évolution d'un compte d'épargne avec ou sans dépôts réguliers. |
 |
Calculateur de prêts – Étudier le remboursement d'un prêt, et comment l'intérêt affecte le remboursement. |
 |
Diagramme circulaire – Explorer des pourcentages et des fractions en utilisant un diagramme circulaire. |
 |
Diagramme de quartiles – Résumer graphiquement des données en utilisant un diagramme de quartiles. |
 |
Diagramme à barres – Créer un histogramme représentant des quantités ou des pourcentages en donnant un titre aux colonnes et en cliquant sur des valeurs. |
 |
Diagramme à nuage de points – Créer une représentation visuelle de données dans un plan et déterminer le coefficient de corrélation. |
 |
Hamlet et le singe – Vérifier que des évènements rares peuvent arriver. |
 |
Histogramme – Résumer des données en créant un diagramme de quartiles ou un histogramme. |
 |
Les prix Whammy – Se rendre compte que différentes méthodes de décompte des votes mènent à des résultats différents. |
 |
Modèle de tirage aléatoire – Représenter le résultat de tirages aléatoires. |
 |
Persister ou changer – Etudier la probabilité de perdre ou de gagner selon le choix de la stratégie. |
 |
Pile ou face – Explorer les concepts de probabilité en jouant à pile ou face. |
 |
Triangle de Pascal – Explorer des motifs créés en créant des configurations dans le triangle de Pascal. |